- Introduction
This monograph will discuss the generation of random numbers mainly in
terms of approaches using cellular automata. In general the theory is equally
applicable to other methods of generating random numbers - however, as the field
of cellular automata has well-established terms and methods for dealing with and
discussing reversibility, and it seems to make sense to discuss the subject in
this domain.
- Reversibility
What is reversibility? A system is reversible if there exists an
inverse rule, which causes the system to run backwards
- and retrace the steps of its temporal evolution.
In terms of cellular automata, it is sufficient to show that its global
function is bijective (one-to-one in both directions) to demonstrate
reversibility.
Conversely, demonstrating two different states that map to the same
state in the next generation is enough to establish that an automaton
is irreversible.
Showing that there exists a "garden of eden" - i.e. a state
with no possible precursor is also sufficient to establish
irreversibility (Richardson, after Moore 1961).
For a finite CA, identifying an initial which never recurs during the future
evolution of the automata is also conclusively demonstrates irreversibility.
- Random Numbers
Historically, both reversible, and irreversible random number generators have
been employed. Distinguishing between the two types seems to have been done
only rather infrequently - a fact which is a little surprising given their
differing properties.
Firstly, irreversible random number generators fail to attain the maximum
possible period for a given internal state. This is simple to prove -
a generator with an internal state of size N bits has a potential period of
2^N. Any irreversible generator will have at least one initial state which
never recurs in the future evolution of the automaton, so we can see that its
period cannot reach 2^N.
Perhaps more significantly, irreversible dynamic systems typically "leak"
information. For every bit destroyed by a reversible generator, it's
period is typically reduced by half. There have been a number of
attempts to quantify the extent to which such systems are likely to
lose the information present in their initial conditions.
In general, an irreversible generator has an expected cycle
length of about sqrt(S), where S is the maximum possible period for a
generator with that quantity of "internal state".
References for this include [V. F. Kolchin, 1986],
[P. Flajolet and A. M. Odlyzko, 1989] and [S. A. Kauffman, 1990].
By contrast a reversible random number generator typically has an expected
cycle of a reversible generator with S possible states has an expected cycle
length of approximately S/2.
This can be seen as follows:
The probability of a cycle occurring does not depend on the length of the cycle -
as the following table should indicate:
| Cycle length |
Probability (workings) |
Result |
| 0 |
0 |
0 |
| 1 |
1 / S |
1 / S |
| 2 |
((S - 1) / S) (1 / (S - 1)) |
1 / S |
| 3 |
((S - 1) / S) ((S - 2) / (S - 1)) (1 / (S - 2)) |
1 / S |
| 4 |
((S - 1) / S) ((S - 2) / (S - 1)) ((S - 3) / (S - 2)) (1 / (S - 3)) |
1 / S |
| N (N <= S) |
((S - 1) / S) ... ((S - (i - 1)) / S - i) ... (1 / (S - (N - 1))) |
1 / S |
It therefore follows that the probability density function representing
the probability of the occurrence of each cycle consists of a series of peaks
at the integers from 1 - N inclusive, each with area 1 / S.
Zero is not included since p(0) = 0.
Given such a distribution, in theory, the expected value lies at the
centre of gravity of the PDF, i.e. at: x = (S + 1) / 2.
This value has received experimental confirmation.
The mathematical notions about the expected period of reversible and irreversible
generators presented here need to be taken with several pinches of salt.
In reality, there's no reason why states should be connected
together at random - and indeed, an intelligently designed generator
should probably try to do better then this. It should be obvious that
reversible generators can also consist entirely of cycles with very
short periods, while irreversible generators can aspire to having a period of P - 1.
A diagram of this should clarify things.
The above equations can probably be considered as a description of
how the period of an existing automata can be expected to scale as
the size of its internal state changes.
While reversibility is usually considered to be an all-or-nothing notion,
it can also be usefully interpreted as a continuum, with irreversibility
being a matter of degree.
Finite irreversible automata cannot leak information forever; they must settle down into cycles where
information is no longer being lost. When they do so, their operation
may be considered to be - to all intents and purposes - reversible.
Some automata settle down onto their attractors rapidly, while others
meander around, slowly losing their precious entropy in the process
before arriving at their limit-cycle.
- Historical review
Many reversible RNGs exist. For example, all
"Linear Feedback Shift Register" generators are reversible.
"Lagged Fibonnaci Generators" are generally - though not always -
reversible, and those "Linear Congruental Generators" which fulfill
Knuth's [Knuth, 1981] various conditions
exhibit the maximum period (for the field 0 - M-1), are thus
demonstrably reversible.
Within the field of cellular automata itself, reversible
random number generators appear less common.
Possibly the first and best-known cellular automata used as a RNG,
the "Wolfram-30" automata [Wolfram 1986] is not reversible.
Neither of the Wolfram-90 nor the Wolfram-130 automata as used by Moshe Sipper,
Marco Tomasso, Mose Zolla, and Mathieu Perrenoud [
Sipper/Tomasso/Zolla/Perrenoud] are reversible.
Rule 90 is described as being S[i](t + 1) = S[i - 1](t) XOR S[i + 1](t).
While this appears to involve the (reversible) XOR operator,
S[i] seems to get discarded, and the result is not reversible.
Rule 150 can be written as:
S[i](t + 1) = S[i - 1](t) XOR S[i](t) XOR S[i + 1](t).
This is the parity operation - it includes only XORs and
involves all the possible cells which might influence the result.
However it is also irreversible. The authors call rules 90 and 150
"simple linear rules" - but this just seems to be a reference
to the fact that their rule tables can be expressed using
XORs.
In fact all the rules used by Sipper/Tomasso/Zolla/Perrenoud (i.e.
rules, 90, 105, 150, 165) produce irreversible dynamics - and consequently
the resulting automata are liable to destroy information. It is not
possible - even by using different spatial combinations of these
rules - to produce a reversible automata.
It was proved by Y. N. Patt [Patt, 1971] that /all/
"non-trivial" Wolfram automata are irreversible. Exhaustive search and the
1D decision procedure for reversibility were employed.
("Trivial" reversible Wolfram automata included 204, 170, 240, 51, 85, 15 -
"UNCHANGED", "SHIFT-LEFT", "SHIFT-RIGHT" and the combinations
of these with "INVERT", respectively.)
Tommaso Toffoli and Norman Margulis proposed a number of pseudo-random number
generators in their (excellent) book, "Cellular Automata Machines"
[Toffoli/Margulis ,1987].
STIR (p.105) is not reversible: it maps neighbourhood states
containing 00000 and 11111 to 00000.
Their NOISE-BOX - being based on STIR - appears
to be subject to the same effect.
MARG-STIR (p.156) is not reversible either, despite using a
partitioning neighbourhood. It comes quite close though - of the 16 states
in each partition, three map to 1111 and two are "Gardens of Eden".
Toffoli and Margulis were experts at the design of reversibile automata - but
their text suggests they didn't put a great deal of effort into the design of
their PRNGs. They refer to STIR as being a "rudimentary" RNG (p.105)
- and - the text of p.70 reads: "With the neighbours in the given order,
the XOR's guarantee that in the long run the soup will yield an even mix of 0's
and 1's []; by putting some non-linearity in the rule, the AND insures that the
system won't get stuck in a short cycle."
This suggests that a bit of a "suck-it-and-see" approach was used in the design
of these generators.
- Diagrams
Here are some diagrams which should assist with the visualization of the characteristics
of the two types of generator under discussion.
Key:
- Red dots indicate individual states of the generator;
- Solid lines indicate final periodic behavior;
- Dotted lines indicate transient paths, traversed before the final oscillator is reached.
Nodes with more than one arrow going into them represent points where information is
irretrievably lost.
Typical reversible and irreversible generators

A typical reversible state map.
|
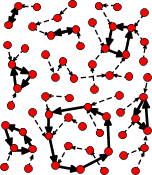
A typical irreversible state map.
|
These diagrams illustrate what you are likely to get if you connect states together randomly.
Taking a seed at random, the reversible generator produces an expected period of roughly S/2,
while the irreversible one has an expected period of roughly sqrt(S).
Reversible generators are not always superior
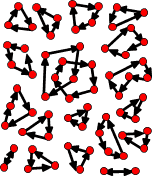
A reversible generator with small periods.
|
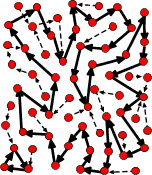
An irreversible generator with a large period.
|
It is far from inevitable that reversible generators exhibit superior
dynamics to irreversible ones:
Two types of "deceptive" irreversible generator
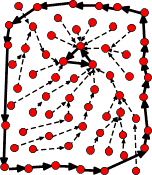
A large period drains a small basin...
while a small period drains a large basin.
|
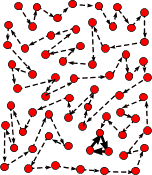
A path through every state...
can still result in a tiny period.
|
The first has a cycle with a large period. However the chance of a randomly chosen
resulting in landing on the cycle is less than 30% - and all other seeds wind up in a
cycle with period three.
The second shows a generator where some seeds result in traversing every node.
When starting with such a seed the generator would initially look random -
but would eventually settle down to a cycle with a very small period.
- Uses for Irreversibility
While irreversible generators "leak" information, and can never attain
the maximum-possible period, they may superficially appear to have some
attractive features.
In particular in cryptography - for example, if you are using a PRNG
as a component of a stream-cypher - it is normally desirable to prevent
one's opponent from predicting an earlier part of a PRNG-stream from the
later part.
One way of making creating difficulties is to ensure that information
used in the earlier part of the message is not even present in the
latter part - by having the information destroyed in the process of
operating the PRNG.
While this might sound attractive, it is important that information is
being lost at the right rate.
If information is destroyed at a rate of one bit per bit of cyphertext output,
the system effectively reduces to a one-time pad - and you need to make sure
that there are as many bits present in your seed as there are in your message.
Of course if information is destroyed any faster than this then it is just
going to waste.
Destroying information more slowly than it is output is the potentially
interesting case. If you destroy it too slowly, then any
advantages of using the method can be lost. For example, the cryptanalyst
may be able to work backwards through your message to the point where a bit
of information is lost from the output of the RNG. Assuming the information
was lost from the internal state relatively recently, he can then search
backwards for it, trying all the various possibilities. After receiving
confirmation from the plaintext about which of these is correct, he can
then continue decoding.
In irreversible systems, the rate of information loss typically
decreases exponentially with time. It's consequently not terribly easy to
transmit a message of any significant length without either wasting lots of
bits or losing any security advantages.
In conclusion, irreversibility may offer some
cryptographical benefits, but there are also disadvantages: namely loss
of randomness as more and more state-information is lost.
Irreversibility makes it harder to predict things that have happened
in the past (i.e. at an earlier point in the encryption process) but it
simultaneously makes it easier to predict things that are likely to
happen in the future. The utility of such an arrangement in cryptography is,
at best, questionable.
If exploiting the advantages without suffering from the disadvantages
could be done the result would be a kind of cross between a PRNG-based
stream cypher and a "one-time pad". As far as we know, the atempt has
not been seriously made.
- Reversible,
"One-Way"
Automata
The question now arises: can you have the benefits of the inability to reverse
an automata /without/ the possible cost of irretreivably losing state information?
The answer seems to be in the affirmative.
In an interesting paper entitled "Reversibility of 2D Cellular Automata is
Undecidable" [Kari, 1990] Jarkko Kari proved a number of
counter-intuitive notions about cellular automata of two dimensions and higher
which use von Neumann-style neighbourhoods.
In particular if follows from his proof that given a class of reversible
automata using the VN neighbourhood, in general, no bound may be placed
on the size of the neighbourhood required by the inverse of that
automaton.
Further, in general, there is no finite effective procedure for locating the
inverse of such a reversible automaton, i.e. there is no algorithm for finding
the inverse rule with a time complexity bounded by a computable function.
This means that finding the inverse of such an automata can be
made extremely difficult.
If we had access to such an automata, it could be used as a component of the
pseudo-random number generator. We could run it forwards in the knowledge that
our opponent will have an extremely difficult time trying to find out how to run
it backwards.
-
"One-Way"
Automata and Public-Key Cryptography
Such "One-way"
automata may be applied in the field of
public-key cryptography. It did not escape the notice of Jarkko Kari that the
existence of the "one-way"
automata he had described
had potentially important implications for public-key cryptography.
He wrote:
"Reversible CA rules can be used to encrypt messages in a natural
way: The plain text is expressed as a configuration of the CA, and the
encryption is done by applying the CA rule rule for a fixed, finite number
of times. The configuration obtained is the cryptotext. One may use
periodic boundary conditions to make the configurations finite in size.
The decryption is done simply by applying the inverse rule to the
cryptotext for the same number of steps. The operations can be
done very efficiently in parallel if proper hardware implementations
are available.
"If one is using an arbitrary two-dimensional, reversible cellular automata,
A to encrypt, and its inverse automaton A' to decrypt messages, then one can
make A public. Making A public does not reveal its inverse A'."
The demands made on the design of automata for use in public-key cryptography
are more restrictive than those required for use in a "one way" random number
generator. For the former, the inverse of the automata must be known, whereas
in the latter case, a proof showing that the inverse of the transition function
existed would suffice.
There's a shortage of one-way functions suitable for use in public-key
cryptography. In the same way that the use of elliptic curves offers
a number of advantages over (say) RSA encryption, so cellular automata
may offer fresh avenues.
- Designing
"One-Way"
Automata
At the moment, relatively little work appears to have been done in the field.
The only worker in the area appears to be the Chinese cryptographer,
[Tao Renji].
His work apparently involves finding two invertable automata, and generating a
composite automata by combining them.
Data is encrypted by passing the data through the composite automaton, and
decrypted by passing the data through the inverses of each of the two automata
that were combined.
The result is a rapid system, but one that requires large keys to operate
securely. This is described further in Bruce Schneier's book, Applied
Cryptography.
We have performed some similar work. See "Public key cryptography using
cellular automata" and "Automata whose inverses
have unboundedly large neighbourhoods" for more details.
- References
Flajolet, P. and Odlyzko, A. M.: "Random Mapping Statistics", Advances in Cryptology - EuroCrypt '89, Springer-Verlag Lecture Notes in Computer Science #434 p. 329-354.
Kari J.: "Reversibility of 2D Cellular Automata is Undecidable", 1990.
Knuth, D. E.: "The Art of Computer Programming, Volume 2: Semi-numerical Algorithms", 1981.
Kauffman, S. A.: "The Origins of Order, Self-Organisation and Selection in Evolution", 1993.
Kolchin, V. F.: "Random Mappings", Optimization Software Inc., New York 1986.
Margulis, N. H., and Toffoli, T.: "Cellular Automata Machines", 1987 MIT Press.
Margulis, N. H., and Toffoli, T.: "Invertible Cellular Automata: A Review", 1990.
Patt, Y. N.: "Injections of neighbourhood size three and four on the set of configurations from the infinite one-dimensional tesselation automata of two-state cells", unpublished, 1971.
Sipper, M., Tomasso, M., Zolla M., and Perrenoud, M.: "Generating High-Quality Random Numbers In Parallel By Cellular Automata".
Sipper, Moshe: "Evolution of Parallel Cellular Machines", Springer, 1997.
Wolfram, S: "Random-Sequence Generation by Cellular Automata", Adv. Applied Math., 1986.